 In his well-known 1968 paper [Phys. Rev. Lett. 21, 1748 (1968)], Ashcroft predicted that hydrogen and hydrogen-dominated materials should be good candidates for high temperature superconductivity with a Tc at about room temperature or even higher. These materials, especially hydrogen, have relatively high phonon frequencies and, according to the McMillan formula, should exhibit high Tc. But in order to be superconducting, hydrogen should be at least metallic, which is theoretically possible at very high pressures. The new work from Naumov and Hemley shows that dense hydrogen can behave as a topological insulator, meaning that it can have metallic surface states even when the bulk material remains insulating. The results are important for the interpretation of existing experimental data on hydrogen conductivity and suggest that dense hydrogen is capable of exhibiting an unusual form of surface conductivity.
In his well-known 1968 paper [Phys. Rev. Lett. 21, 1748 (1968)], Ashcroft predicted that hydrogen and hydrogen-dominated materials should be good candidates for high temperature superconductivity with a Tc at about room temperature or even higher. These materials, especially hydrogen, have relatively high phonon frequencies and, according to the McMillan formula, should exhibit high Tc. But in order to be superconducting, hydrogen should be at least metallic, which is theoretically possible at very high pressures. The new work from Naumov and Hemley shows that dense hydrogen can behave as a topological insulator, meaning that it can have metallic surface states even when the bulk material remains insulating. The results are important for the interpretation of existing experimental data on hydrogen conductivity and suggest that dense hydrogen is capable of exhibiting an unusual form of surface conductivity.
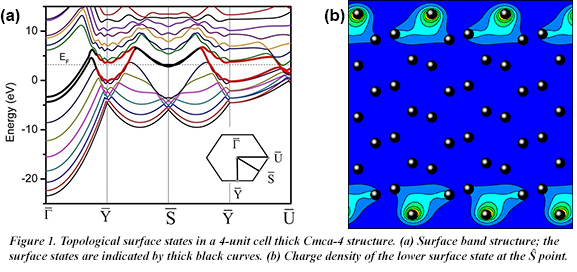
The existence of surface states in many theoretically predicted phases of compressed hydrogen can be derived from their bulk band structures, as for topological insulators, by simply calculating the so-called Zak’s phase along the direction perpendicular to the surface, for all possible in-surface k-vectors, k ǁ. If for a given k ǁ the phase is π, then the surface state exists; if the phase 0, the surface state does not exist. Using this approach it is predicted, for example, that in its Cmca-4 phase hydrogen should have (001) surface states everywhere in the two-dimensional surface Brillouin zone, but not in the vicinity of the Ῡ point (Fig. 1a). The direct calculations of surface states show that this is indeed the case. It is seen that they actually exist everywhere, but not just around the Ῡ points, in accordance with the Zak’s phase calculations. The system is metallic because the surface bands cross the Fermi level. The charge density corresponding to the lower surface state at Ŝ is shown in Fig. 1b; the density is localized at the top and bottom atomic layers of the slab with a normal ǁ z.
 It is well known that 2D or quasi-2D systems can be potentially good superconductors. Examples include the cuprates in which superconductivity is confined to planar CuO2 layers. Highly oriented pyrolytic graphite provides another example, in which superconductivity is localized at the 2D interfaces. From the results of the present work, the existence of such “surface superconductivity” is predicted to exist in compressed hydrogen [I. Naumov and R. J. Hemley, Phys. Rev. Lett. 117, 206403 (2016)].
It is well known that 2D or quasi-2D systems can be potentially good superconductors. Examples include the cuprates in which superconductivity is confined to planar CuO2 layers. Highly oriented pyrolytic graphite provides another example, in which superconductivity is localized at the 2D interfaces. From the results of the present work, the existence of such “surface superconductivity” is predicted to exist in compressed hydrogen [I. Naumov and R. J. Hemley, Phys. Rev. Lett. 117, 206403 (2016)].
